Reward Systems in Sports

Who’s the Fairest of Them All?

Benjamin Baumer and Sarah Susnea

Smith College

Sep 27, 2025

I wrote a thing…

On fairness in sports (Baumer 2024)

Equality vs. equity

Examples

  • Bartneck and Moltchanova (2024)
  • De Veaux, Plantinga, and Upton (2022)
  • Sauer, Cseh, and Lenzner (2024)
  • Pollard, Noble, and Pollard (2022)
  • Guyon (2018)
  • Arlegi and Dimitrov (2020)
  • Scelles, François, and Valenti (2024)
  • Martens and Starflinger (2022)
  • …

Fairness in Machine Learning

COMPAS: recidivism scores

race two_year_recid risk_score n
African-American 0 High 345
African-American 0 Low 1169
African-American 1 High 843
African-American 1 Low 818
Caucasian 0 High 106
Caucasian 0 Low 1175
Caucasian 1 High 230
Caucasian 1 Low 592
  • \(Y\): Did they recidivate (within 2 years)
  • \(\hat{Y}\): Did COMPAS label them high risk?
  • \(A\): Protected class (i.e., race)

ProPublica (Angwin et al. 2016)

https://github.com/propublica/compas-analysis

Prediction fails differently for Black Defendants

Error Type White African-American
Labeled Higher Risk, But Didn't Re-Offend 23.5 44.9
labeled Lower Risk, Yet Did Re-Offend 47.7 28.0
  • ❌ COMPAS fails to demonstrate error rate parity
  • ❌ COMPAS fails to demonstrate demographic parity

Northpointe

https://go.volarisgroup.com/rs/430-MBX-989/images/ProPublica_Commentary_Final_070616.pdf

\[ \Pr{(\neg Y | \hat{Y}, W)} = 0.409 \approx \Pr{(\neg Y | \hat{Y}, B)} = 0.370 \\ \Pr{(Y | \neg \hat{Y}, W)} = 0.288 \approx \Pr{(Y | \neg \hat{Y}, B)} = 0.448 \]

Statistical criteria for fairness

(Barocas, Hardt, and Narayanan 2023)

“Dozens” of statistical criteria for fairness boil down to 3:

  • Independence
  • Separation
  • Sufficiency

Independence

  • aka disparate impact

\[ \left| \Pr(\hat{Y} | W) - \Pr(\hat{Y} | B) \right| < \epsilon \,, \] where \(\epsilon\) is a small positive constant (typically \(\epsilon < 0.2\))

  • ❌ COMPAS FAILS:

\[ \left| 0.348- 0.588 \right| = 0.210 > \epsilon \,, \]

Separation

  • aka error rate parity

\[ \left| \Pr(\hat{Y} | Y, W) - \Pr(\hat{Y} | Y, B) \right| < \epsilon \\ \left| \Pr(\hat{Y} | \neg Y, W) - \Pr(\hat{Y} | \neg Y, B) \right| < \epsilon \]

  • ❌ COMPAS FAILS:

\[ \left| 0.523 - 0.720 \right| = 0.197 < \epsilon \\ \left| 0.235 - 0.488 \right| = 0.253 > \epsilon \]

Sufficiency

  • aka well-calibration

\[ \left| \Pr(Y | \hat{Y}, W) - \Pr(Y | \hat{Y}, B) \right| < \epsilon \,, \]

  • ✅ COMPAS PASSES:

\[ \left| 0.591 - 0.630 \right| = 0.039 < \epsilon \]

Kleinberg’s impossibility theorem

Unless the base rates are the same across the groups, you can’t satisfy all three criteria simultaneously (Kleinberg, Mullainathan, and Raghavan 2016)

COMPAS summary

  • ProPublica: COMPAS is biased because it lacks error rate parity
  • Northpointe: Yeah, but it’s well-calibrated!
  • Kleinberg: But since the base rates aren’t the same:
    • …you’re both right
    • …and you’re both wrong
  • So is the algorithm fair or not??

Introducing faireR

  • leverages yardstick and mlr3fairness
  • computes independence, separation, and sufficiency
    • mean absolute difference across groups
  • visualizations
  • data sets
  • tidyverse-friendly

Using faireR

library(faireR)
compas_grp <- compas_binary |>
  mutate(
    y = two_year_recid,
    y_hat = factor(ifelse(decile_score >= 7, 1, 0))
  ) |>
  group_by(race)

# compute fairness for COMPAS
compas_grp |>
  fairness_cube()
# A tibble: 1 × 3
  independence separation sufficiency
         <dbl>      <dbl>       <dbl>
1        0.214      0.186      0.0509

Fairness IRL

The narrow view

People with similar qualifications should be treated similarly

  • individual fairness
  • Ex: the meritocracy, race-blind admissions, etc.

The broad view

People of equal ability and ambition should have similar chances

  • fairness across groups
  • Ex: all schools should be equally well-funded

The middle view

Adjust for past injustice (that caused the differences in qualifications) at the time of opportunity

What does this have to do with sports?

Providing vocabulary, Ex 1

Instead of:

two equal pairs should have as close to an equal chance of winning as possible. (Pollard, Noble, and Pollard 2022)

  • We have a broad view of fairness
  • We focus on sufficiency (aka well-calibration)

Providing vocabulary, Ex 2

Instead of:

A swimmer with no arms should be able to compete against a swimmer with one or two arms…If two athletes with the same disability compete, the more skilled and fitter should win. (Bartneck and Moltchanova 2024)

  • We have a middle view of fairness
  • Focus on separation and sufficiency

Providing vocabulary, Ex 3

Instead of:

We present two methods to distribute prize money across gender based on the individual performances w.r.t. gender-specific records. We suppose these “across gender distributions” to be fair, as they suitably respect that women generally are slower than men. (Martens and Starflinger 2022)

  • We have a middle view of fairness
  • Focus on independence

Called strikes in MLB

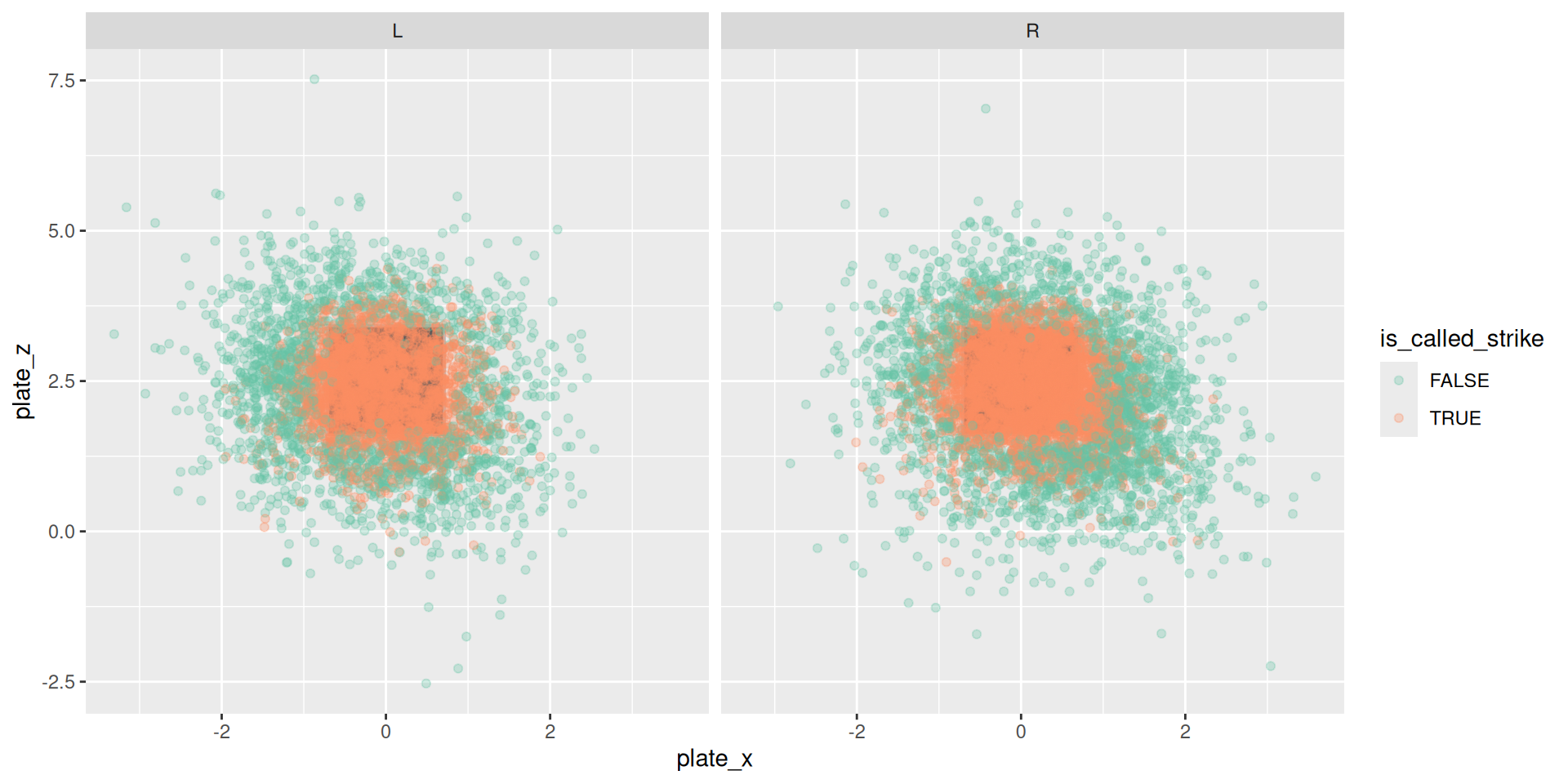
Are umpires fair to LHH?

csas_grp <- csas25 |>
  mutate(
    y = factor(is_within_strike_zone),
    y_hat = factor(is_called_strike)
  ) |>
  group_by(stand)

csas_grp |>
  fairness_cube()
# A tibble: 1 × 3
  independence separation sufficiency
         <dbl>      <dbl>       <dbl>
1       0.0104     0.0496      0.0856
  • \(Y\): Was it a strike?
  • \(\hat{Y}\): Was it called a strike?
  • ✅ Independence
  • ✅ Separation
  • ✅ Sufficiency

A simple Hall of Fame classifier

https://baseballwithr.wordpress.com/2014/11/18/building-a-hall-of-fame-classifier-2/

hof_dt <- tree_spec |>
  fit(
    as.factor(inducted) ~ tH + tHR + mvp + gg + tW + tSO + tSV + cy,
    data = candidates
  )
  • See Mills and Salaga (2011) for a more serious attempt…

Is the classifier fair w.r.t. batters and pitchers?

hof2025 |>
  mutate(is_pitcher = tSO > 100) |>
  group_by(is_pitcher) |>
  fairness_cube()
# A tibble: 1 × 3
  independence separation sufficiency
         <dbl>      <dbl>       <dbl>
1      0.00322    0.00520      0.0323

✅

Is the classifier fair w.r.t. starters and relievers?

hof2025 |>
  mutate(
    is_pitcher = tSO > 100,
    is_reliever = tSV > 50
  ) |>
  filter(is_pitcher) |>
  group_by(is_reliever) |>
  fairness_cube()
# A tibble: 1 × 3
  independence separation sufficiency
         <dbl>      <dbl>       <dbl>
1      0.00446      0.275      0.0821

❌

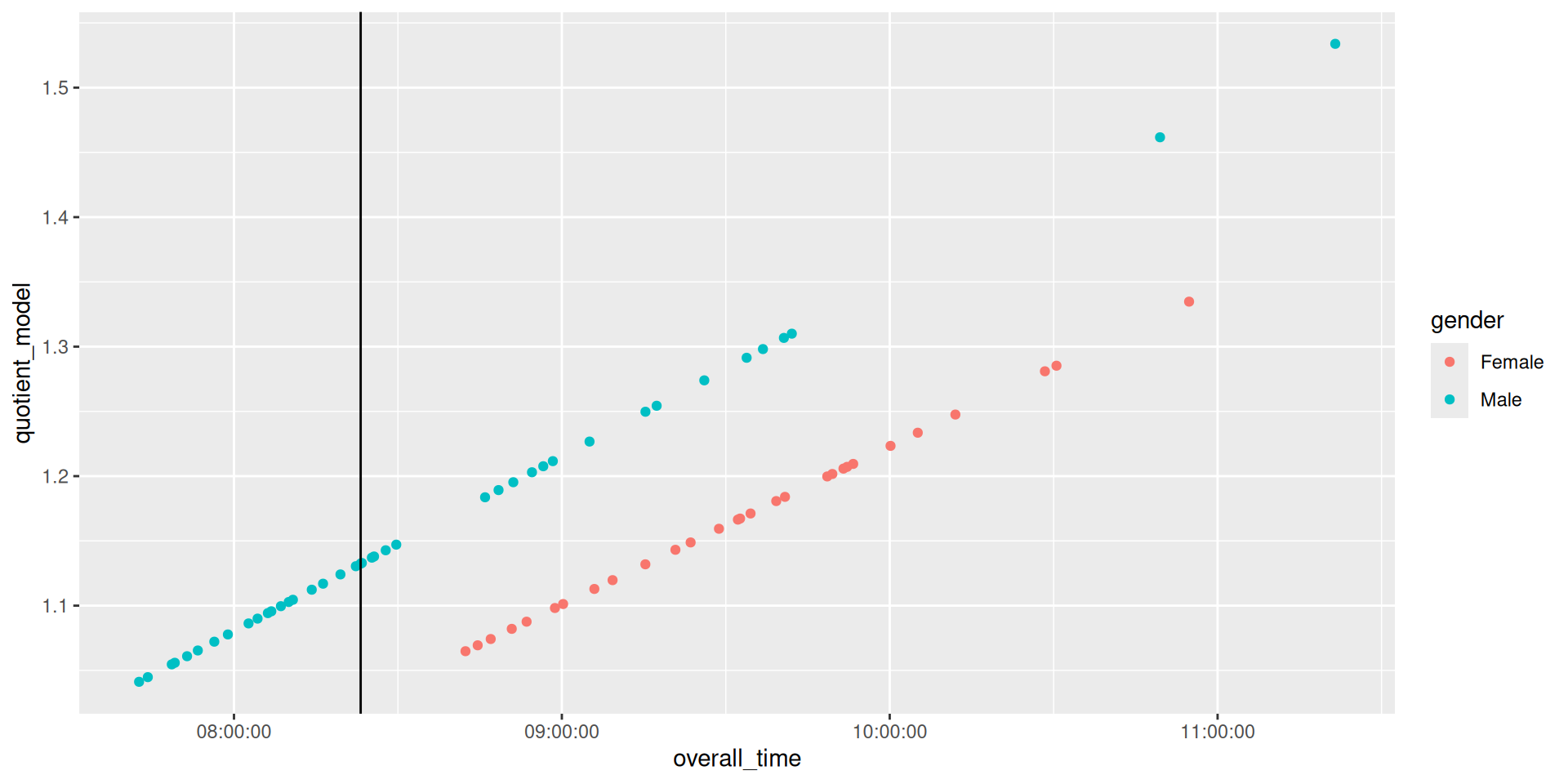
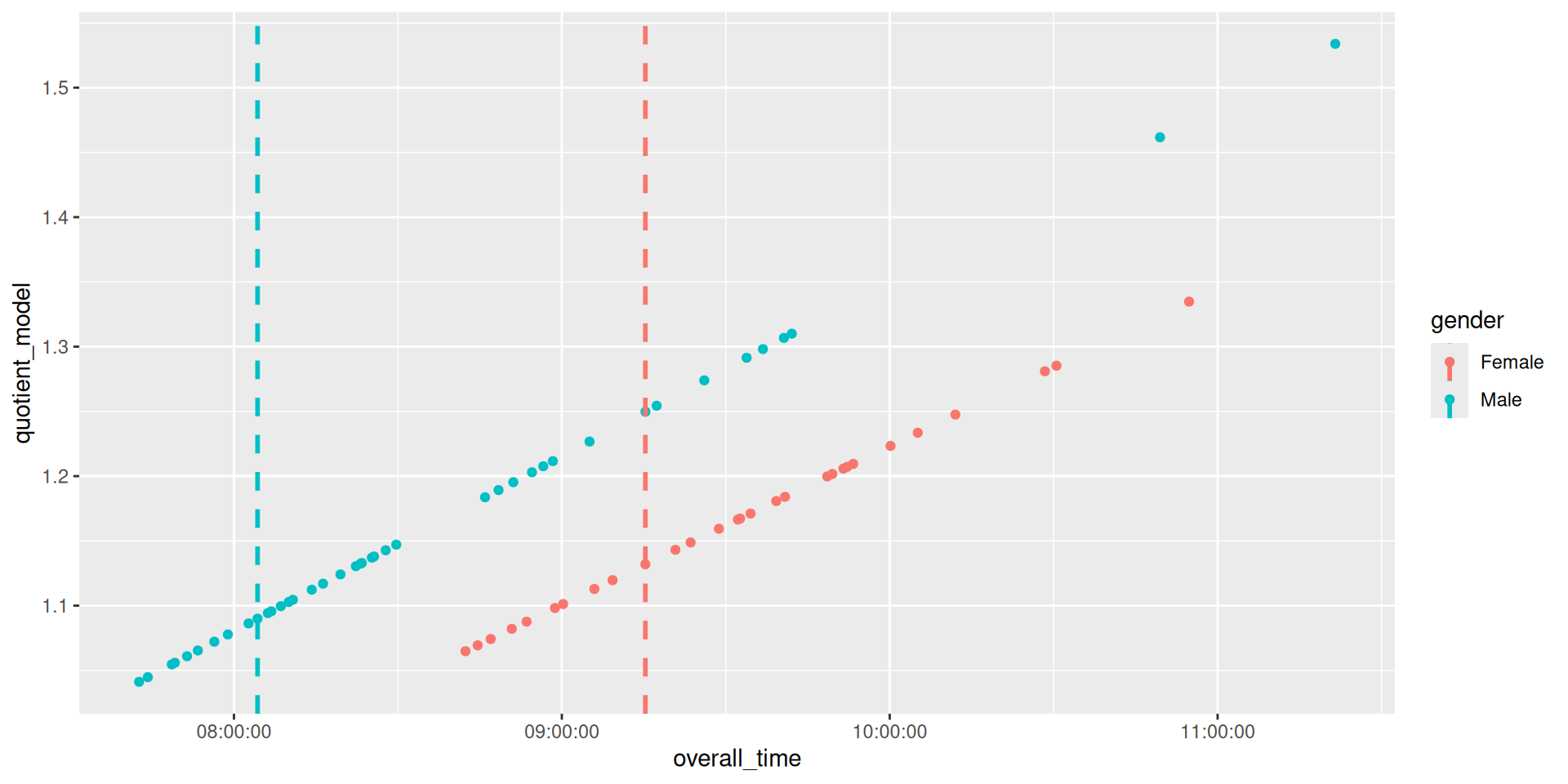
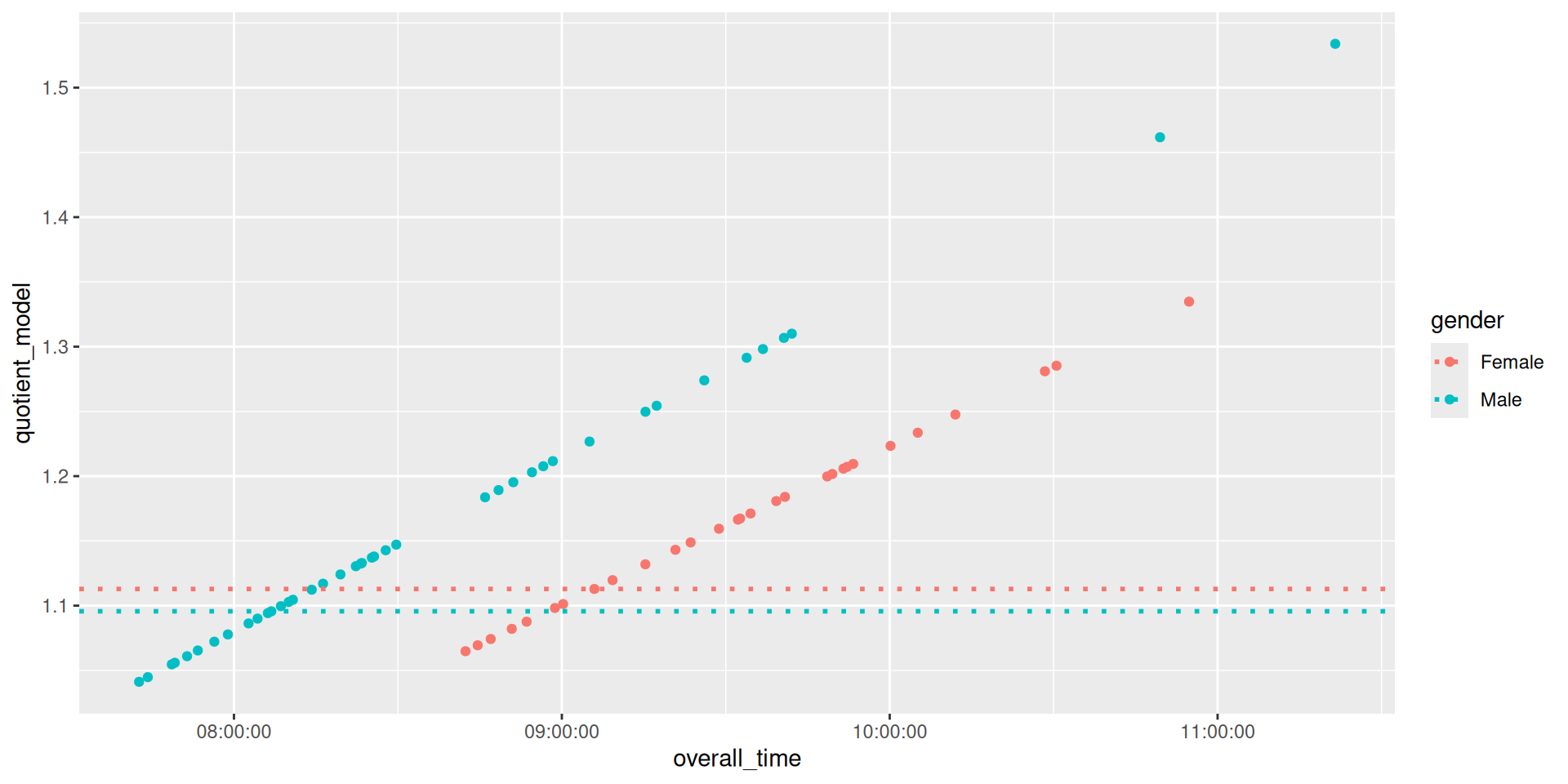
Ironman Texas

https://www.coachcox.co.uk/imstats/race/2148/results/

Award prizes to:

  • Naive: Fastest 20, regardless of gender
  • Status Quo: Fastest 10 in each gender division
  • Martens: Fastest 20 in relation to gender-specific world records
ironman_grp <- ironman |>
  mutate(
    fastest20 = factor(dense_rank(overall_time) <= 20),
    status_quo = factor(division_rank <= 10),
    martens = factor(dense_rank(quotient_model) <= ifelse(gender == "Male", 12, 8))
  ) |>
  group_by(gender)

Texas Ironman naive

Texas Ironman status quo

Texas Ironman proposed

Texas Ironman fairness

ironman_grp |>
  fairness_cube(truth = fastest20, estimate = status_quo)
# A tibble: 1 × 3
  independence separation sufficiency
         <dbl>      <dbl>       <dbl>
1        0.101         NA          NA
ironman_grp |>
  fairness_cube(truth = status_quo, estimate = martens)
# A tibble: 1 × 3
  independence separation sufficiency
         <dbl>      <dbl>       <dbl>
1        0.126        0.3       0.118

Future work

  • Visualize fairness in 2D
    • ROC curves
    • Calibration plots
  • Visualize fairness in 3D
  • Distance metric for overall fairness?
  • Is mean absolute difference the best measure?
  • Find additional suitable applications

References

Angwin, Julia, Jeff Larson, Surya Mattu, and Lauren Kirchner. 2016. “Machine Bias.” ProPublica; ProPublica. https://www.propublica.org/article/machine-bias-risk-assessments-in-criminal-sentencing.
Arlegi, Ritxar, and Dinko Dimitrov. 2020. “Fair Elimination-Type Competitions.” European Journal of Operational Research 287 (2): 528–35. https://doi.org/10.1016/j.ejor.2020.03.025.
Barocas, Solon, Moritz Hardt, and Arvind Narayanan. 2023. Fairness and Machine Learning: Limitations and Opportunities. MIT Press. https://mitpress.mit.edu/9780262048613/fairness-and-machine-learning/.
Bartneck, Christoph, and Elena Moltchanova. 2024. “Fair World Para Masters Point System for Swimming.” Journal of Quantitative Analysis in Sports 20 (2): 147–77. https://doi.org/10.1515/jqas-2023-0051.
Baumer, Benjamin S. 2024. “Editor’s Note: On Fairness in Sports Analytics.” Journal of Quantitative Analysis in Sports. De Gruyter. https://doi.org/10.1515/jqas-2023-0103.
De Veaux, Richard, Anna Plantinga, and Elizabeth Upton. 2022. “Are the Handicaps Fair? Age and Participation Effects in the Dipsea Race.” Chance 35 (4): 40–49. https://doi.org/10.1080/09332480.2022.2145138.
Dieterich, William, Christina Mendoza, and Tim Brennan. 2016. “COMPAS Risk Scales: Demonstrating Accuracy Equity and Predictive Parity Performance of the COMPAS Risk Scales in Broward County.” Northpointe Inc. Research Department. https://go.volarisgroup.com/rs/430-MBX-989/images/ProPublica_Commentary_Final_070616.pdf.
Guyon, Julien. 2018. “What a Fairer 24 Team UEFA Euro Could Look Like.” Journal of Sports Analytics 4 (4): 297–317. https://doi.org/10.3233/JSA-180219.
Kleinberg, Jon, Sendhil Mullainathan, and Manish Raghavan. 2016. “Inherent Trade-Offs in the Fair Determination of Risk Scores.” arXiv Preprint arXiv:1609.05807. https://arxiv.org/abs/1609.05807.
Martens, Maren, and Verena Starflinger. 2022. “Alternative Prize Money Distributions for Higher Gender Equity in Sports.” In International Conference on Operations Research, 333–39. Springer. https://doi.org/10.1007/978-3-031-24907-5_40.
Mills, Brian M, and Steven Salaga. 2011. “Using Tree Ensembles to Analyze National Baseball Hall of Fame Voting Patterns: An Application to Discrimination in BBWAA Voting.” Journal of Quantitative Analysis in Sports 7 (4). https://doi.org/10.2202/1559-0410.1367.
Pollard, Graham, Ken Noble, and Geoff Pollard. 2022. “New Scoring System to Reduce Unfairness in Men’s Doubles.” Journal of Sports Analytics 8 (4): 291–98. https://doi.org/10.3233/JSA-220607.
Sauer, Pascal, Ágnes Cseh, and Pascal Lenzner. 2024. “Improving Ranking Quality and Fairness in Swiss-System Chess Tournaments.” Journal of Quantitative Analysis in Sports 20 (2): 127–46. https://doi.org/doi:10.1515/jqas-2022-0090.
Scelles, Nicolas, Aurélien François, and Maurizio Valenti. 2024. “Impact of the UEFA Nations League on Competitive Balance, Competitive Intensity, and Fairness in European Men’s National Team Football.” International Journal of Sport Policy and Politics 16 (3): 519–37. https://doi.org/10.1080/19406940.2024.2323012.